数学的产生与发展过程蕴含着丰富的数学文化。
(1)以“导数及其应用”教学为例，说明在数学教学中如何渗透数学文化；(6分)
(2)阐述数学文化对学生数学学习的作用。(9分) 

案例：
下列是两位教师“复数概念”引入的教学片段：
【教师甲】
为了解决x2-2=0在有理数集中无解，以及单位正方形对角线的度量等问题，在初中，把有理数集扩充到了实数集。
x2+1=0在实数集中有解吗?类比初中的做法，我们如何做呢?看来，又需要扩充数系。
数学家引入了i，使i是方程x2+1=0的一个根，即使x2=-1，把这个新数i添加到实数集中去，就会得到一个新数集，记作A，那么方程x2+1=0在A中就有解x=i了。这样我们就引入了一个新数。
【教师乙】
16世纪，意大利数学家卡尔达诺在解决“求两个数，使其和为10，积为40”时，认为这两个

这样我们就引入了一个新数。
这节课我们学习了复数的表达形式a+bi(a，b∈R)。当然，复数还有其他表示法，在后续的学习中我们会学习到。
问题：
(1)请分析这两位教师教学引入片段的特点；(12分)
(2)复数还有三角表示法，请简述三角表示法的意义。(8分)

某位教师设计了高中数学必修内容“分层抽样”的教学目标为：
①通过实例，了解分层抽样的特点、适用范围及分层抽样的必要性，掌握分层抽样的操作步骤：
②体会分层抽样、简单随机抽样以及系统抽样的区别与联系，提升整体把握知识的能力。
基于上述内容，完成下列任务：
(1)基于教学目标①，设计一个实例，总结分层抽样的步骤，并说明设计意图；(21分)
(2)基于教学目标②，简要说明简单随机抽样、系统抽样以及分层抽样各自特点及适用范围。(9分) 

矩阵的秩为（ ）

A.0

B.1

C.2

D.3 

当x→x0时，与x-x0。是等价无穷小的为()。

A.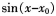

B.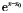

C.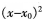

D.|n|x-x0|